Matrici: calcolare determinante, inversa, autovalori, autovettori, ecc

Come calcolare online le proprietà delle matrici quali determinante, traccia, rango, trasposta, autovalori, autovettori, inversa, pseudo-inversa, polinomio caratteristico, diagonalizzazione

In Algebra Lineare hanno una particolare importanza le matrici, tabelle formate da un certo numero di celle in una griglia, che sono la rappresentazione matematica di una trasformazione lineare.

Le righe orizzontali di una matrice sono chiamate semplicemente righe mentre quelle verticali si chiamano colonne. Una matrice mxn vuol dire che è formata da m righe e n colonne. Quando le matrici hanno lo stesso numero di righe e colonne vengono dette quadrate. Spesso per le matrici si usa anche la notazione simbolica A_ij dove ij sono le variabili che indicano rispettivamente il numero di riga e di colonna dell'elemento. A₃₅ rappresenta p.e. l'elemento che si trova nella terza riga e nella quinta colonna. 

L'algebra delle matrici è quell'insieme di operazioni che possono essere fatte con le matrici quali somma, prodotto, moltiplicazione per uno scalare. Le matrici possono essere interpretate anche come sistemi di equazioni lineari dove ciascun elemento è il coefficiente della rispettiva incognita.

L'algebra matriciale è quindi importante per la risoluzione dei sistemi di equazioni ma anche in moltissime altre discipline della matematica come la meccanica quantistica. Il Determinante di matrici quadrate è un dato fondamentale per sapere se un sistema di equazioni abbia o meno delle soluzioni.

La Traccia di una matrice è la somma dei valori della diagonale formata dagli elementi A_ii . L'Inversa di una matrice è la matrice che moltiplicata con la prima dà per risultato la matrice Unità, formata da tutti 1 nella diagonale e da tutti 0 per quello che riguarda gli altri elementi.

Una matrice può essere anche interpretata come trasformazione di vettori. Quando un vettore viene trasformato in un altro vettore, che differisce dal primo solo per un fattore numerico, si parla di Autovettore. Per trovare gli Autovettori si ricava il Polinomio Caratteristico della matrice per poi trovarne gli Autovalori.

Il determinante di una matrice 2x2 si trova moltiplicando i numeri della matrice in diagonale. In questo caso abbiamo D= A₁₁ x A₂₂ - A₁₂ x A₂₁. Esiste una regola mnemonica, creata da Sarrus, per calcolare il determinante delle matrici 3x3, ma non ci sono regole altrettanto semplici per le matrici con un rango superiore.

Gli studenti che si trovano a dover trovare determinante e altri parametri matriciali, possono però usufruire di tool online che servono proprio a questo scopo. Ho pubblicato sul mio Canale Youtube un video tutorial in tal senso.

In questo post vedremo due tool online che ci permetteranno di risolvere i problemi matriciali con pochi click e in modo immediato. Se si deve trovare il determinante, la matrice inversa o gli autovalori di una matrice, esclusivamente numerica, allora basterà utilizzare il tool Online Matrix Calculator.

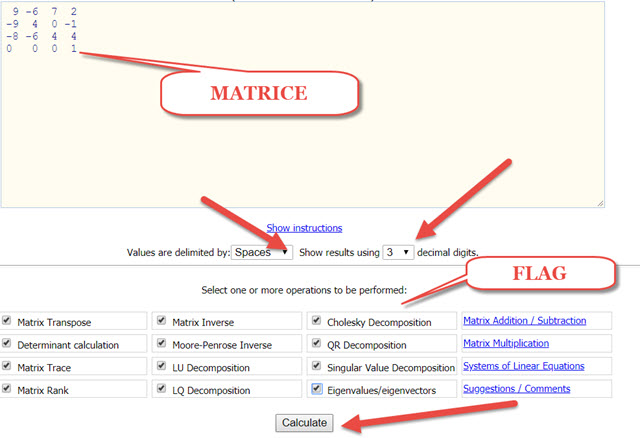
In Values are delimited by si può scegliere se separare i valori della matrice con spazi, tabulazioni o virgole mentre più a destra si seleziona il numero di decimali da visualizzare nei risultati (da 0 a 15).

In basso si mette la spunta alle operazioni da compiere sulla matrice che abbiamo digitato. Si può trovare la Matrice Trasposta, il Determinante, la Traccia, il Rango, la Matrice Inversa, la Matrice Pseudo-Inversa ovvero di Moore-Penrose, gli Autovalori, gli Autovettori,  Decomposizione QR, ecc.

Si clicca su Calculate per ottenere i risultati desiderati.

Online Matrix Calculator permette di trovare in un click tutti i risultati delle principali operazioni matriciali. Nello stesso strumento ci sono i link per sommare, sottrarre e moltiplicare le matrici oltre a uno strumento per risolvere i sistemi di equazioni lineari. Il tool funziona però solo con i valori numerici.

MATRICI CON VALORI LETTERALI

Se stiamo lavorando a un problema con matrici non solo numeriche ma anche letterali, per la loro risoluzione online bisogna usare uno strumento più potente, come quello messo a disposizione da Wolframalpha, il motore di ricerca computazionale che ha pure rilasciato una applicazione per calcoli scientifici veramente eccellente.

Dopo aver aperto la Home di Wolframalpha si clicca su Algebra, tra le numerose categorie di calcoli presenti sotto la casella di ricerca. Nella pagina che si apre si cerca Matrices che sono nella colonna di destra. Conviene cliccare su More Examples per visualizzare la sintassi da utilizzare per il calcolo matriciale.

In Matrix Properties sono visibili degli esempi esemplificativi di come inserire le matrici.

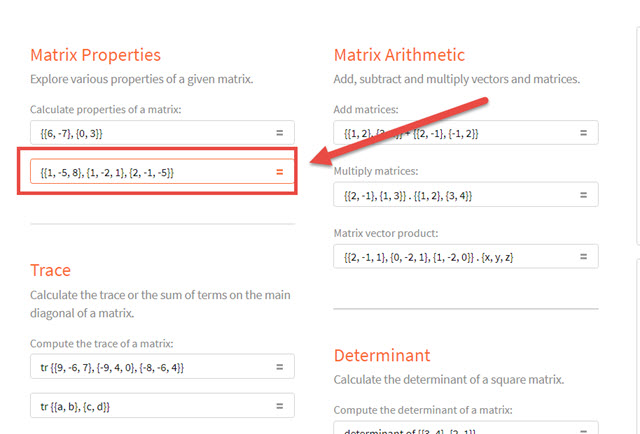
In sostanza le matrici si inseriscono tra delle parentesi graffe e ciascuna riga sarà mostrata, sempre tra parentesi graffe, con i valori separati da virgole. Le righe poi saranno separate sempre da una virgola. Si clicca sul segno di uguale, per vedere il risultato della matrice di esempio. Si potranno però sostituire i valori della matrice con quella da calcolare e se ne potranno anche modificare il numero delle righe e delle colonne.

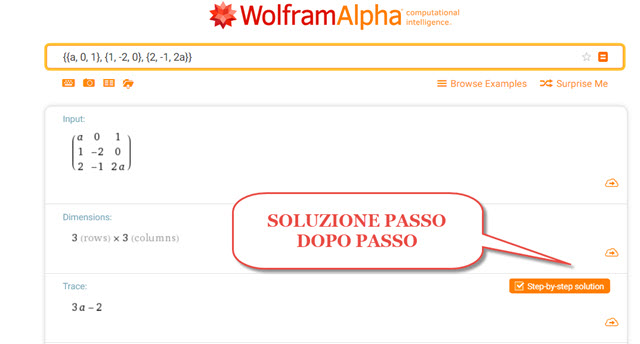
Per ogni operazione effettuata viene mostrato il risultato con accanto il pulsante Step-by-step solution, per visualizzare la soluzione passo dopo passo. Questa opzione però è riservata solo agli utenti Pro a pagamento. Si possono comunque visualizzare tali passaggi con la modica spesa di 3,19€, mediante l'app WolframAlpha per Android. Prima di installarla però informatevi bene perché alcuni utenti hanno lamentato nelle loro recensioni che i passaggi step-by-step non vengono più mostrati, cosa che però a me non risulta nella mia app.

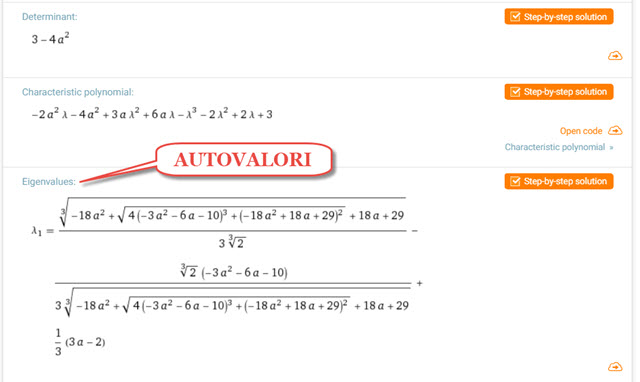
Si va sulla icona uguale (=) e ci verrà mostrato l'input della matrice, insieme alla Traccia, al Rango, al Polinomio Caratteristico, agli Autovalori, gli Autovettori e alla matrice per la Diagonalizzazione.